1. (IDECAN) Numa fazenda existem duas raças de gado:
girolando e nelore. A respeito da quantidade de gados dessa fazenda, sabe-se
que:
girolando e nelore. A respeito da quantidade de gados dessa fazenda, sabe-se
que:
• o número de gados nelore supera o número de gados
girolando em 36 unidades; e,
• aumentando-se o número de gados da raça girolando em 23
unidades, obtém-se 6/7 da quantidade de gados nelore.
Considerando as informações dadas, pode-se concluir que
nesta fazenda existem quantos gados no total?
a) 138.
b) 142.
c) 146.
d) 154.
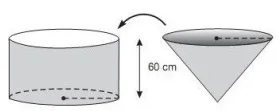
possuem alturas iguais a 60 cm e bases circulares com o mesmo raio. O cone está
completamente cheio de água e o cilindro está vazio, apoiado sobre uma mesa
horizontal. Despejando-se toda a água contida no cone dentro do cilindro, o
nível de água no cilindro ficará a uma altura, contado a partir de sua base
inferior, igual a:
b) 30 cm.
c) 20 cm.
d) 15 cm.
e) 10 cm.
de um cilindro reto. Sabendo que o vaso tem 20cm de altura e a circunferência
da base do vaso tem raio igual a 5cm, de quantos litros de água ela precisará
para enchê-lo? (Use π = 3 e 1m3 = 1000L)
a) 1,05L
B) 150L
C) 15L
D) 0,150L
E) 1,5L
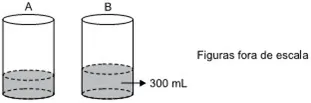
óleo, A e B, que estão abertas e com óleo em seu interior. O óleo que está na
lata A corresponde a 1/4 do seu volume total, e a lata B contém 300 mL de óleo,
conforme mostram as figuras.
mais 300 mL para que a lata B fique totalmente cheia. O volume total da lata B,
em mL, é
b) 600.
c) 700.
d) 800.
e) 900.
figura.
base medindo ambos 6 cm, utiliza-se o cubo de aresta 6 cm.
madeira nesse processo é igual a
a) 43,78 cm3.
b) 44,35 cm3.
c) 45,12 cm3.
d) 46,44 cm3.
receber ordem para projetar um tanque de combustível com capacidade de 71
litros, criou cinco versões, listadas a seguir.As medidas internas dos
recipientes são inteiras e foram apresentadas apenas algumas dessas medidas:
Alfa: um prisma retangular com base 13 dm²
Beta: um cubo
Gama:um prisma retangular junto com um cubo de aresta 4 dm
Delta: um cilindro
Epsílon: um cilindro junto com um cubo de aresta 4dm
capacidade será igual à do tanque solicitado?
a) Alfa.
b) Beta.
c) Gama.
d) Delta.
e) Epsílon.
igual ao raio de sua base. Se a razão entre o volume do cilindro, dado em
metros cúbicos, e a sua área total, dada em metros quadrados, é igual a 2
metros, então a área lateral do cilindro, em m² , é igual a
a) 128π
b) 64π
c) 48π
d) 32π
e) 16π
Beta: um cubo
Gama:um prisma retangular junto com um cubo de aresta 4 dm
Delta: um cilindro
Epsílon: um cilindro junto com um cubo de aresta 4dm
capacidade será igual à do tanque solicitado?
a) Alfa.
b) Beta.
c) Gama.
d) Delta.
e) Epsílon.
igual ao raio de sua base. Se a razão entre o volume do cilindro, dado em
metros cúbicos, e a sua área total, dada em metros quadrados, é igual a 2
metros, então a área lateral do cilindro, em m² , é igual a
a) 128π
b) 64π
c) 48π
d) 32π
e) 16π
cilíndrico possui raio igual a 3 metros. Esse tanque foi colocado dentro de um
tanque esférico, cujo raio é igual a 5 metros.
O volume máximo, em metros cúbicos, que o tanque cilíndrico
pode ter é
a) 90 π
b) 72 π
c) 54 π
d) 45 π
e) 36 π
igual ao raio de sua base. Se a razão entre o volume do cilindro, dado em
metros cúbicos, e a sua área total, dada em metros quadrados, é igual a 2
metros, então a área lateral do cilindro, em m2 , é igual a
b) 64
c) 48
d) 32
e) 16
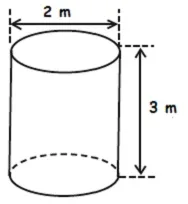
sua casa, o Sr. José construiu um sistema de captação de água das chuvas. Essa
água será armazenada em uma cisterna cilíndrica cujas dimensões internas são
três (3) metros de altura e dois (2) metros de diâmetro, conforme esquema na
figura a seguir.
V = π . R2 . H (para efeito de cálculo, adote : π
= 3,14)
Poucos dias após o término da construção da cisterna, quando
ela ainda estava totalmente vazia, choveu dois dias seguidos, o que deixou o
Sr. José muito contente, pois ele observou que:
, o que fez o nível da água na cisterna atingir a marca de 72 cm;
• no segundo dia, o índice pluviométrico foi de 30 mm/m2
.
Considere que:
• não foi retirada água da cisterna nesse período;
• no interior da cisterna entrou apenas a água da chuva;
• o índice pluviométrico e a altura da coluna de água na
cisterna são grandezas diretamente proporcionais e;
• cada 1 m3 equivale a 1000 L.
ela ainda estava totalmente vazia, choveu dois dias seguidos, o que deixou o
Sr. José muito contente, pois ele observou que:
, o que fez o nível da água na cisterna atingir a marca de 72 cm;
• no segundo dia, o índice pluviométrico foi de 30 mm/m2
.
Considere que:
• não foi retirada água da cisterna nesse período;
• no interior da cisterna entrou apenas a água da chuva;
• o índice pluviométrico e a altura da coluna de água na
cisterna são grandezas diretamente proporcionais e;
• cada 1 m3 equivale a 1000 L.
Sendo assim, o Sr. José determinou que o volume de água
captado/armazenado na cisterna após esses dois dias de chuva foi de
aproximadamente:
a) 942 litros
b) 1840 litros
c) 3140 litros
d) 3960 litros
e) 4145 litros
captado/armazenado na cisterna após esses dois dias de chuva foi de
aproximadamente:
a) 942 litros
b) 1840 litros
c) 3140 litros
d) 3960 litros
e) 4145 litros
GABARITO
1C / 2C / 3E / 4D / 5D / 6C / 7A / 8B / 9A / 10E
Deixe um comentário mais abaixo avaliando esta atividade, é só rolar a página! Ficaremos felizes com seu comentário.
Inscrever-se
0 Comentários
mais antigos
