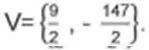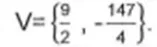Questões de Concurso de Matemática sobre Função do 2º Grau com Gabarito (II)

 1. (LEGALLE CONCURSOS) O ponto de mínimo do gráfico da função y = 1/3 x² + 3x -30 é dado por:
a)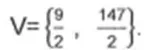 
b)
c) 
d) 
e) 

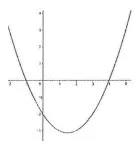
2. (LEGALLE CONCURSOS) A figura abaixo apresenta o gráfico de uma função do segundo grau do tipo y = ax² + bx + c. Sobre seus , coeficientes, podemos afirmar que:

a) a > 0, b > 0 e c > 0.
b) a > 0, b < 0 e c > 0.
c) a > 0, b > 0 e c < 0.
d) a > 0, b < 0 e c < 0.
e) a< 0, b > 0 e c < 0.

3. (CONSULPAN) Quantos números inteiros apresenta a interseção entre as soluções das inequações: x² + 2x – 35 ≤ 0 e –x² – 4x + 12 > 0?
a) 5
b) 6
c) 7
d) 8
e) 9

4. (FUNDATEC) Um carrinho de uma montanha russa, em um determinado momento do percurso, percorre uma trajetória descrita por y = – x² + 10 x, onde y é a altura em metros. Qual a altura máxima atingida por esse carrinho?
a) 18 m
b) 22 m
c) 24 m
d) 25 m
e) 50 m

5. (IDECAN) A função do 2º grau y = ax² – 4x – 16 apresenta uma de suas raízes igual a 4. A outra raiz é
a) 1
b) – 1
c) 2
d) – 2
e) 3

6. (FUNDATEC) A figura abaixo representa o gráfico obtido através da seguinte equação de segundo grau: x² + 3x + 2. O ponto marcado equivale ao valor de x do vértice da parábola. Qual é o valor incógnito?    

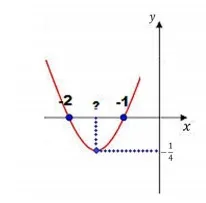
a) 3/2                                                                                      
b) 0,75
c) 1/2
d) – 3/2
e) – 0,75

7. (GUALIMP) Ao resolver a equação do 2º grau abaixo, os valores deverão ser:
ƒ(x) = x² – 3x + 2

a) -2 e 2.
b) 4 e -2.
c) 4 e 2.
d) 2 e 1.

8. (GUALIMP) A função que originou o gráfico a seguir trata-se de uma função:

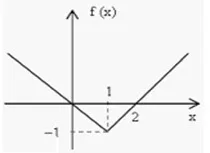
a) Logarítmica.
b) Delta.
c) Modular.
d) Quadrática.

9. (INSTITUTO UNIFIL) Dada a função quadrática, ƒ(x) = x² – 3x – 4, quais os valores em que ƒ(x) = 0 ?
a) {1,4}
b) {-2,3}
c) {-2,1}
d) {-1,4}

10. (IBADE) Os pontos no eixo das abcissas x que marca o encontro das funções y = x² + 2x + 3 e y = 2x + 7 é:
a) 3 e 4
b) 3 e 7
c) 4 e 7
d) 3 e 2
e) -2 e +2

---

+ Questões de Concurso de Matemática

Confira nossa página repleta de conteúdos semelhantes, especialmente desenvolvidos para esse público escolar. Materiais pedagógicos de alta qualidade, cuidadosamente preparados pelos produtores do Tudo Sala de Aula. Clique agora e escolha o tema da aula!

Acesse outros exercícios