Questões de Concurso de Matemática sobre Função do 1º Grau com Gabarito

Download do conteúdo disponível no final da publicação

1. (MS CONCURSOS) O valor máximo que a função f(x) = 2x + 3 cos (2x) no intervalo em que x ∈ [0, π] é igual a:
a) π – 3
b) π + 3
c) 2π – 3
d) 2π + 3

2. (INSTITUTO CONSULPAN) Sejam dois conjuntos A e B definidos por: A {-2,-1, 0, 1, 2, 3} e B { y|y é natural} e uma função f : A  B definida por: f(x) = 2x + 1. Qual das alternativas representa o produto dos elementos do conjunto imagem de f?
a) 12
b) 105
c) 210
d) 315

3. (FAUEL) Para quais valores a função f(x) = 3x-12 assume valores negativos?
a) Para valores menores que 4.
b) Para valores menores ou iguais a 4.
c) Para valores maiores ou iguais a 4.
d) Para valores maiores que 4.

4. (INSTITUTO CONSULPAN) As informações contextualizam a questão. Leia-as atenciosamente.

“Altair é um empresário do ramo de alimentos e inaugurou um novo restaurante de comida árabe que oferece um serviço de entrega de esfirras no valor de R$ 2,50 a unidade, mais uma taxa de entrega fixa no valor de R$ 8,00.”

De acordo com o serviço de entrega do restaurante de Altair, qual é a função que representa o valor “v” de uma entrega em relação à quantidade “x” de esfirras encomendadas por um cliente?
a) v = 10,5x
b) v = 8x + 2,5
c) v = 2,5x + 8
d) v = 2,5x – 8

5. (COVEPE-UFAL) Em Matemática, define-se ponto fixo como o ponto que não é alterado por uma aplicação (função). Mais precisamente falando, se f: é uma função, um ponto fixo de f é todo ponto x* tal que f(x*) = x*.

Dadas as afirmativas a respeito de pontos fixos de funções,

I. A função f(x) = x2 + 1 não tem ponto fixo. 
II. A função f(x) = 2x – 1 tem dois pontos fixos. 
III. A função f(x) = x3 + x tem um único ponto fixo.

verifica-se que está(ão) correta(s)
a) I, apenas.
b) II, apenas.
c) I e III, apenas.
d) II e III, apenas.
e) I, II e III.

6. (AMEOSC) Sobre uma função de primeiro grau (y = ax + b), assinale a alternativa correta:
a) Será decrescente à medida que o valor da variável “y” diminui e a variável “x” aumenta.
b) Será decrescente à medida que o valor da variável “y” aumenta a variável “x” diminui.
c) Será crescente sempre que o sinal à frente de “ax” for negativo.
d) Será crescente sempre que “b” for positivo.

7. (GUALIMP) O número médio de peças produzidas por minuto em uma fábrica varia de acordo com o número de horas trabalhadas segundo a função dada a seguir:

p(t) = 14t – t 2 

Determine o total de peças produzidas caso a fábrica funcione exatamente o número de horas que determina a maior produtividade média possível.
a) 49 peças.
b) 343 peças.
c) 2.940 peças.
d) 20.580 peças.

8. (GUALIMP) O gráfico abaixo representa uma função do primeiro grau na forma f(x) = ax + b, onde a e b  .

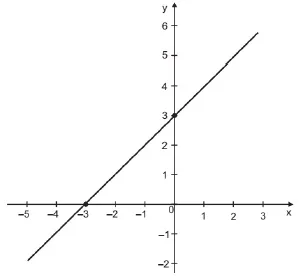
Analisando esse gráfico, os coeficientes a e b são, respectivamente:
a) Negativo e positivo.
b) Negativo e negativo.
c) Positivo e negativo.
d) Positivo e positivo.

9. (GUALIMP) Dado que f(x) = | x + 1 |, analise os itens abaixo.

I. Trata-se de uma função do 1º grau.
II. O domínio é o conjunto dos números reais positivos.
III. A imagem é o conjunto dos números reais positivos e o zero. IV. Se x = –3, f(x) = 2.

Dos itens acima
a) Apenas I está correto
b) II e III estão corretos.
c) III e IV estão corretos.
d) Apenas IV está correto.

10. (LEGALLE CONCURSOS) Sendo f(x) =

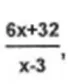
Qual o valor da imagem de f(8)?
a) 10.
b) 12.
c) 14.
d) 16.

+ Conteúdos com Questões de Matemática para Concursos

Confira nossa página repleta de conteúdos semelhantes, especialmente desenvolvidos para esse público escolar. Materiais pedagógicos de alta qualidade, cuidadosamente preparados pelos produtores do Tudo Sala de Aula. Clique agora e escolha o tema da aula!

Acesse outros exercícios