Prova online de Matemática 8º e 9º ano sobre Função Polinomial do 2° Grau: Gráficos, Construção e Análise.
É necessário resolver todas as questões para gerar o resultado. Boa sorte!
Exibir respostas somente após resolver todas as questões:
—
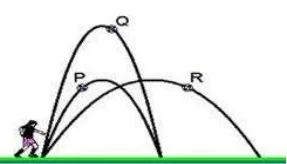
(SMERJ) Um jogador de futebol está participando de um treino em que estão sendo avaliadas a potência e a altura de seu chute.
Ao observar as parábolas formadas pelo lançamento da bola, determine a letra que representa a maior altura alcançada pela bola
—
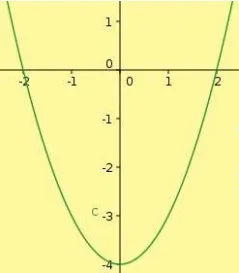
(SMERJ) Dada a função quadrática y = x² – 4 = 0, determine o ponto mínimo da parábola.
—
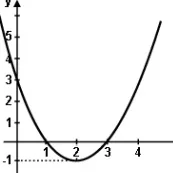
(SMERJ) A parábola representada na imagem é o gráfico de uma função quadrática. As raízes dessa função são:
—
(SMERJ) Uma indústria de sucos tem sua produção diária P, em garrafas, variando com o número de operadores em serviço x , de acordo com a função P(x) = x² + 50x + 2.000. Qual será a produção de sucos quando o número de operadores for de 30 pessoas?
—
(SMERJ) Uma bola de ping-pong é largada do alto de um edifício e cai em direção ao solo. Sua altura h em relação ao solo, t segundos após o lançamento, é dada pela expressão h = –5t² + 125. Após quantos segundos do lançamento a bola atingirá o solo?
—
(SMERJ) Uma função quadrática é dada pela lei y = ( z – 4).x² + x. Para quais valores de z o gráfico dessa função é uma parábola de concavidade para cima?
—
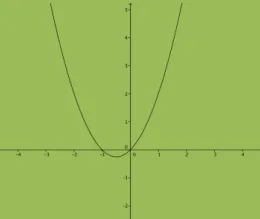
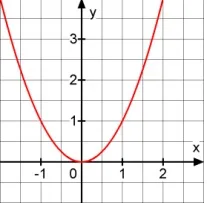
(SMERJ) Qual das funções representa o gráfico ao lado?
—
(SMERJ) Numa sapataria de modelos exclusivos, o custo diário da produção de x sapatos é dado por P (x) = x² – 40x + 410, em que P é a produção de sapatos e x o valor em reais. Qual o custo mínimo da produção diária?
—
(SMERJ) Segundo afirmam os fisiologistas, o número de batimentos cardíacos por minuto, para um indivíduo em repouso e sadio, varia em função da temperatura, em graus Celsius, e é expresso pela função B (t) = 0,1t² – 4t + 90, em que B é o número de batimentos e t é a temperatura. A que temperatura um indivíduo sadio, em repouso, terá 90 batimentos?
—
(SMERJ) Um menina lançou uma peteca para cima e observou que sua trajetória era dada pela função h(x) = – x² + 4x +20, em que h é a altura em metros e x o tempo em segundos. Qual será a altura máxima atingida por essa peteca?
Sua nota:
Você acertou de questões
Nível de aprendizagem: