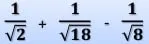Prova online de Matemática 8º e 9º ano sobre Racionalização de Denominadores.
É necessário resolver todas as questões para gerar o resultado. Boa sorte!
Exibir respostas somente após resolver todas as questões:
—
(SMERJ) A velocidade com que um corpo em queda livre chega ao solo, partindo de uma altura h, é dada pela expressão V = √2gh , segundo Galileu Galilei. (Na superfície da Terra, a aceleração da gravidade g é de, aproximadamente, 10 m/s²) Suponha que um corpo caia de uma torre de 10 m de altura. Qual a sua velocidade ao chegar ao solo?
—
(SMERJ) Os lados de uma janela medem respectivamente: 54 e 150. Então, quanto é o perímetro dessa janela?
—
Certo azulejo que Joana quer comprar possui um formato quadrado e o lado 6- √7. Joana mediu a área aproximada desse azulejo e descobriu que mede:
—
(SMERJ) Se você tivesse a expressão 1 / (4∛2), qual seria o fator racionalizante?
—
(SMERJ) Tiago aprendeu que para racionalizar o denominador de uma fração devemos multiplicar os termos dessa fração por um fator racionalizante, de modo a obter uma nova fração equivalente com denominador sem radical. Então, que fator ele deve utilizar para racionalizar a fração que está na figura:
Marque o fator racionalizante.
—
(SMERJ) Das alternativas abaixo representa a solução da expressão:
—
(SMERJ) Qual será a representação da expressão: 1 / ∛7, com o denomidador racionalizado?
—
(SMERJ) Racionalizando o denominador da expresão: 10 / (2 + √3), teríamos:
—
(SMERJ) Certo desenho é formado por 4 triângulos retângulos, cortados de azulejos decorados, dos quais um dos catetos mede 2√5 cm. Qual deve ser a medida do outro cateto para que esse desenho tenha área de 60 cm²?
—
(SMERJ) Sabendo que a área de certo painel triangular mede 46 m² e a altura mede (7 – √3) m, calcule a medida da base.
Sua nota:
Você acertou de questões
Nível de aprendizagem: