Nossa equipe preparou uma excelente Atividade de Matemática sobre Perímetros para os estudantes do 5° ano. Conhecer e aplicar esse conceito é essencial não apenas para resolver problemas matemáticos, mas também para compreender a importância da geometria na nossa vida cotidiana. Venha conhecer, baixar gratuitamente e aplicar em sala de aula!
Você pode baixar esta atividade em PDF no final, pronta para impressão.
1. Observe a imagem de um barco na malha quadriculada a seguir.
Considerando que a medida do lado de cada quadrado é igual a 1cm, calcule o perímetro do barco representado.
a) 37cm.
b) 36cm.
c) 35cm.
d) 34cm.
2. Em uma gincana escolar, uma das provas a serem realizadas era a do labirinto. A equipe de organização montou o labirinto no formato hexagonal utilizando tábuas de MDF e a parte externa foi coberta por um adesivo amarelo, como mostra a figura.
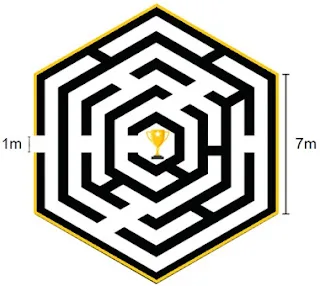
Utilizando o conceito de perímetro, calcule a medida do adesivo utilizado no contorno do labirinto e marque a alternativa correta.
a) 43 metros.
b) 42 metros.
c) 41 metros.
d) 36 metros.
3. Ricardo é pedreiro e vai construir um muro ao redor de sua casa. Após fazer as medidas, ele fez a anotação de que o terreno tem formato retangular com 25 metros de comprimento e 9 metros de largura. Qual o perímetro do terreno de Ricardo?
a) 34 metros.
b) 43 metros.
c) 59 metros.
d) 68 metros.
4. Raquel gosta de fazer exercícios físicos e costuma correr ao redor da quadra esportiva que fica próxima à sua casa. Veja abaixo.
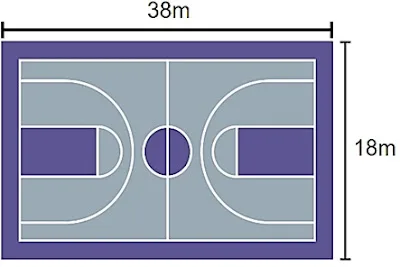
Ao completar 6 voltas, quantos metros Raquel terá percorrido?
Resposta:_________
5. João tem um terreno grande e um espaço reservado para plantio de legumes e verduras. Esse espaço tem formato pentagonal de lados iguais medindo 12 metros cada e será cercado com uma tela. Quantos metros de tela serão necessários para cercar a horta de João?
a) 48m.
b) 52m.
c) 60m.
d) 64m.
6. Edson comprou um terreno retangular e resolveu cercar com arame farpado. Observe as medidas de uma volta do arame que ele utilizou.
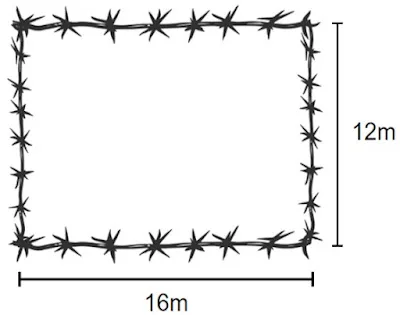
a) Qual o perímetro desse terreno?
Resposta:___________
b) Quantos metros de arame farpado ele vai utilizar se cercar o terreno com 5 voltas de arame?
Resposta:___________
7. Observe as figuras na malha quadriculada abaixo.
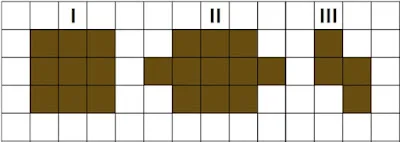
Qual a soma dos perímetros das figuras, considerando que a medida do lado de cada quadradinho é igual a 1cm?
a) 24cm.
b) 34cm.
c) 36cm.
d) 38cm.
8. Bruno tem uma academia de luta e utilizou cordas vermelhas para cercar o ringue. Veja a imagem a seguir.
Tendo em vista que o ringue tem o formato de um quadrado e que apresenta a medida de um lado, quantos metros de corda Bruno utilizou para deixar o ringue como mostra na imagem?
a) 24 metros.
b) 48 metros.
c) 72 metros.
d) 78 metros.
9. Lia planeja contornar um quadro branco que tem em casa com alumínio. Ao fazer as medidas, ela constatou que o quadro tinha 150cmX120cm. Quantos metros de alumínio Lia precisa comprar para fazer a borda do quadro?
a) 54 metros.
b) 50,4 metros.
c) 5,4 metros.
d) 5 metros.
10. Tales vai inaugurar um supermercado na cidade. Para o evento, ele vai utilizar o espaço do estacionamento que será cercado por uma fita. Veja o espaço demarcado abaixo e a medida de um lado da figura formada.
Quantos metros de fita serão necessários para cercar a área demarcada por Tales?
a) 135m.
b) 120m.
c) 105m.
d) 90m.
Acesse outros conteúdos semelhantes.
.png)
Atividade em PDF está mais abaixo, pronta para IMPRESSÃO e GABARITO!
Não compartilhe o PDF, se precisar, compartilhe o link desta atividade!
Por Geiciane Santos
Tudo Sala de Aula
Atividade feita com carinho por Tudo Sala de Aula!😊
GABARITO
1B / 2C / 3D / 4. 672 m. / 5C / 6. a) 56m. b) 280m. / 7D / 8C / 9C / 10B
