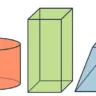
📝 Excelente Atividade de Matemática sobre Volumes para os estudantes do 8º e 9º ano. Entender e calcular volumes é fundamental para o desenvolvimento do raciocínio matemático e a resolução de problemas do cotidiano. Conheça, baixe e aplique em sala de aula!
Download e planejamento do conteúdo disponíveis no final da publicação.

1. Joana vai encher a sua caixa d’água com formato de um paralelepípedo com dimensões 1,2 m de comprimento, 0,8 m de largura e 1,5 m de altura. Qual o volume de água que essa caixa pode armazenar?
a) 1,44 m³.
b) 1,5 m³.
c) 2,1 m³.
d) 2,4 m³.
2. Veja abaixo a caixa de canecas de porcelana que a Gráfica MS personalizados comprou.
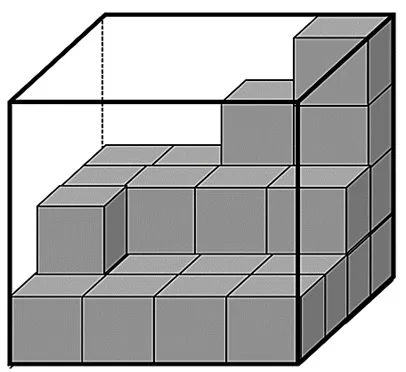
Sabendo que a caixa estava completamente cheia e que já foram retiradas algumas canecas para personalização, quantas canecas havia na caixa?
a) 28
b) 36
c) 64
d) 75
3. Um pote de sorvete com formato de paralelepípedo retângulo possui as dimensões de 12 cm, 5 cm e 8 cm. Qual é a capacidade máxima de sorvete que este pote comporta?
a) 480 ml.
b) 520 ml.
c) 600 ml.
d) 680 ml.
4. Lucinha dispõe de 7 litros de suco para servir aos 38 participantes de uma reunião de trabalho. Sabendo que ela comprou copos descartáveis de 180 ml e que irá servi-los até a medida 175 ml, responda:
a) Quantos copos Lucinha conseguirá servir?
b) Após servir todos os participantes, ainda sobrará suco? Se sim, quantos mililitros?
c) Se Lucinha servisse em copos de 200 ml, completamente cheios, o suco seria suficiente para encher quantos copos?
5. Um reservatório de água possui o formato de um cubo de aresta medindo 2 metros.
a) Calcule o volume do reservatório em metros cúbicos (m³).
b) Quantos litros de água este reservatório consegue armazenar?
6. Observe o caixote que Gleison comprou para organizar seus queijos para revenda.
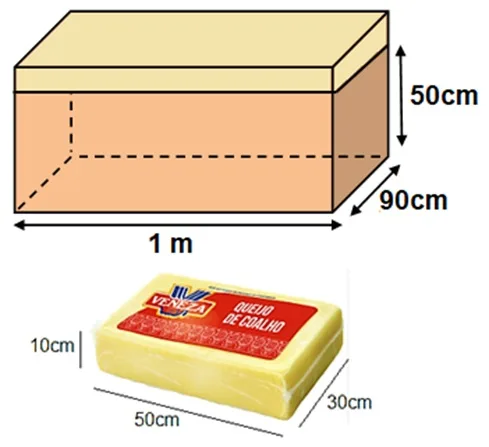
Considerando que seus queijos são blocos retangulares de dimensões 10cm, 50cm e 30cm, quantos desses queijos Gleison consegue armazenar no seu caixote?
a) 25
b) 30
c) 32
d) 45
7. Observe o paralelepípedo retângulo de dimensões indicadas por a, b e c.
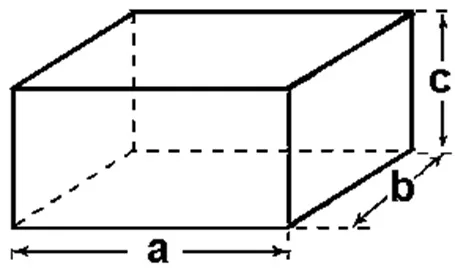
A fórmula correta para calcular o volume desse paralelepípedo retângulo é
a) V = 3⋅(a . b. c)
b) V = a.b.c
c) V = a + b + c
d) V =
8. Em uma fábrica de sorvetes, há um tanque cilíndrico de armazenamento que estando completamente cheio comporta 225 litros de sorvete. A fábrica precisa transferir todo esse sorvete para potes retangulares, cujas dimensões são 6,4 cm de altura, 13 cm de largura e 18 cm de comprimento, conforme a figura.

A quantidade mínima de potes que a fábrica precisará para armazenar todo o sorvete é
a) 120 potes.
b) 125 potes.
c) 148 potes.
d) 167 potes.
9. Elionai foi a uma madeireira comprar blocos de madeira para algumas encomendas de móveis. Veja as dimensões de três tipos de blocos disponíveis na madeireira.
Bloco I – 80 cm de comprimento, 20 cm de altura e 40 cm de largura;
Bloco II – 60 cm de comprimento, 50 cm de altura e 30 cm de largura;
Bloco III – 60 cm de comprimento, 40 cm de altura e 20 cm de largura.
Sabendo que Elionai vai comprar somente dois blocos e que deseja o maior volume de madeira possível, quais blocos ele deve escolher?
a) Blocos I e II.
b) Blocos I e III.
c) Blocos II e III.
d) Os blocos I e II possuem o mesmo volume dos blocos II e III.
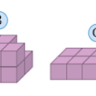
10. Considerando que a aresta de cada cubo da figura mede 4 cm, determine o volume do cubo maior, em cm³.
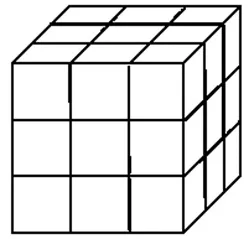
11. Maria está organizando um evento e precisa calcular a quantidade de sorvete que caberá em cada modelo de recipiente que dispõe. Para isso, ela deve realizar algumas conversões de unidades de medida de volume.
Observe os recipientes que Maria possui e seus respectivos volumes, e ajude-a a fazer as conversões para mililitros.
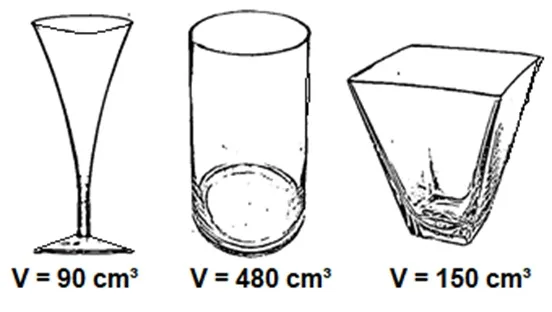
a) Capacidade da taça cônica: ________________
b) Capacidade do copo cilíndrico:______________
c) Capacidade da caneca tronco de pirâmide: ________
12. Um tanque com formato de bloco retangular de dimensões 15cm, 22cm e 30cm está com 30% de sua capacidade preenchida. Qual o volume de água que falta para que o tanque fique com sua capacidade total preenchida?
a) 2 970 cm³.
b) 6 700 cm³.
c) 6 930 cm³.
d) 9 900 cm³.
+ Conteúdos de Matemática para o 8º e 9º ano
Confira nossa página repleta de conteúdos semelhantes, especialmente desenvolvidos para esse público escolar. Materiais pedagógicos de alta qualidade, cuidadosamente preparados pelos produtores do Tudo Sala de Aula. Clique agora e escolha o tema da aula!
Planejamento para o professor
Objeto do conhecimento: Volume de blocos retangulares
Objetivo da Aula: Compreender e aplicar a fórmula do volume de blocos retangulares, desenvolvendo a habilidade de resolver situações-problema envolvendo medidas de espaço em unidades cúbicas.
Habilidade da BNCC: (EF08MA20) Compreender e reconhecer a relação entre um litro e um decímetro cúbico, a relação entre litro e metro cúbico para resolver e elaborar problemas envolvendo o cálculo de capacidade de recipientes. (EF08MA21) Resolver e elaborar problemas, de diferentes contextos, que envolvam o cálculo do volume de recipiente cujo formato é o de um bloco retangular. (EF09MA19) Resolver e elaborar problemas, de diferentes contextos, que envolvam medidas de volumes de prismas e de cilindros retos, inclusive com uso de expressões de cálculo.
Por favor, não compartilhe o PDF!
Reiteramos que todo o conteúdo do site Tudo Sala de Aula é original, produzido por equipe própria. Portanto, este material, assim como os demais, não pode ser publicado em sites pessoais ou copiado para a criação de apostilas para venda. Pirataria é crime! Estamos de olho! (Lei 9.610/98)
Gostou? Deixe um comentário!😍

Por Eleí dos Santos
Licenciada em Matemática, especialista em Didática da Matemática, Psicopedagogia e Educação Especial.
O conteúdo foi revisado e certificado pela equipe de Redação do Tudo Sala de Aula.